Preissmann Slot Theory
In Riemannian geometry, a field of mathematics, Preissman's theorem is a statement that restricts the possible topology of a negatively curvedcompactRiemannian manifoldM. Specifically, the theorem states that every non-trivial abelian subgroup of the fundamental group of M must be isomorphic to the additive group of integers, Z.[1][2]
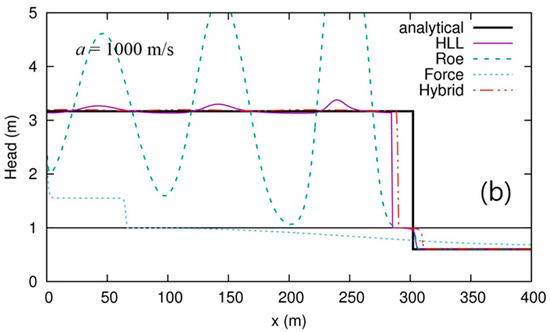

More practically, based on the traditional Preissmann model, some numerical simulation models were constructed for drainage networks, including a model based on an introduced virtual slot on the crown of the pipe to treat a separated gas–liquid flow 16,17; a model capable of simulating transient flows in closed conduits, ranging from free. Means of the free-surface set of equations (Preissmann slot model). The original concept of the negative Preissmann slot is proposed to simulate sub-atmospheric pressure. This model is shown to be particularly well suited for the simulation of bubbly and intermittent flows. Keywords: hydraulics, Preissmann slot, homogeneous equilibrium model. The models are based on the interface-tracking approach, the Preissmann slot concept and a standard closed pipe method of characteristics code. TPA results show good agreement with the results.

Preissmann Slot Theory Definition
One of the most popular and earliest methods is the Preissmann slot method (generally abbreviated as PSM), named after its innovator engineer Preissmann. In the PSM, a virtual narrow slot above the crowns of the pipe allows the system to remain in an open channel flow condition even when the conduit becomes completely full.
A corollary of Preissman's theorem is that the n-dimensional torus, where n is at least two, admits no Riemannian metric of negative sectional curvature.

References[edit]
Preissmann Slot Theory Game
- ^Ruggiero, Rafael Oswaldo (2000), 'Weak stability of the geodesic flow and Preissman's theorem', Ergodic Theory and Dynamical Systems, 20 (4): 1231–1251, doi:10.1017/S0143385700000663, MR1779401.
- ^Grant, Alexander (2012), Preissman's theorem(PDF), University of Chicago Mathematics Department.